选择题 共15道
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15阅读程序 共18道
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33完善程序 共10道
34 35 36 37 38 39 40 41 42 43P370 2021年CCF非专业级别软件能力认证第一轮 (CSP-S)提高级C++语言试题-练习
选择题 共15道
01 在 Linux 系统终端中,用于列出当前目录下所含的文件和子目录的命令为( ) 2分
02
二进制数 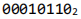
和 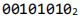
的和为( )
2分
03 在程序运行过程中,如果递归调用的层数过多,可能会由于( )引发错误。 2分
04 以下排序方法中,( )是不稳定的 2分
05 以比较为基本运算,对于 2n 个数,同时找到最大值和最小值,最坏情况下需要的最小的比较次数为( )。 2分
06
现有一个地址区间为 0~10 的哈希表,对于出现冲突情况,会往后找第一个空的地址存储(到 10 冲突了就从
0 开始往后),现在要依次存储(0,1, 2,3,4,5,6,7),哈希函数为 h(x)=x2 mod 11。请问 7 存储在
哈希表哪个地址中( )。
2分
07 G 是一个非连通简单无向图(没有自环和重边),共有 36 条边,则该图至少有( )个点 2分
08 令根结点的高度为 1,则一棵含有 2021 个结点的二叉树的高度至少为( )。 2分
09 前序遍历和中序遍历相同的二叉树为且仅为( ) 2分
10 定义一种字符串操作为交换相邻两个字符。将“DACFEB”变为 “ABCDEF”最少需要( )次上述操作。 2分
11
有如下递归代码
solve(t, n):
if t=1 return 1
else return 5*solve(t-1,n) mod n
则 solve(23,23)的结果为( )。
2分
12
斐波那契数列的定义为:F1=1,F2=1,Fn=Fn-1+Fn-2 (n>=3)。现在用如下程序来计算斐波那契数列的第 n
项,其时间复杂度为( )。
F(n):
if n<=2 return 1
else return F(n-1) + F(n-2)
2分
13 有 8 个苹果从左到右排成一排,你要从中挑选至少一个苹果,并且不能同时挑选相邻的两个苹果,一共有( )种方案。 2分
14
设一个三位数 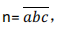
a, b, c 均为 1~9 之间的整数,若以 a、 b、 c 作为三角形的三条边可以构成等腰三
角形(包括等边),则这样的 n 有( )个
2分
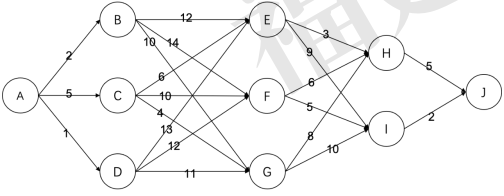
15
有如下的有向图,节点为A, B, … , J, 其中每条边的长度都标在图中。则节点A 到节点J 的最短路径长度为
()。
2分

阅读程序 共18道
16
第 16 - 21 题 组合题

假设输入的所有数的绝对值都不超过 1000,完成下面的判断题和单选题:
将第 21 行中 t 的类型声明从 int 改为 double,不会影响程序运行的结果。( )
1.5分

17 将第 26、27 行中的“/ sqrt(t) / 2”替换为“/ 2 / sqrt(t)”,不会影响程序运行的结果。( ) 1.5分
18 将第 28 行中的“x * x”改成“sq(x)”、“y * y”改成“sq(y)” ,不会影响程序运行的结果。( ) 1.5分
19 当输入为“0 0 0 1 1 0 0 1”时,输出为“1.3090”。( ) 1.5分
20 当输入为“1 1 1 1 1 1 1 2”时,输出为( )。 3分
21 这段代码的含义为( )。 3分
22
第 22 - 27 题 组合题


假设输入的所有数的绝对值都不超过 1000,完成下面的判断题和单选题:
程序总是会正常执行并输出两行两个相等的数。( )
1.5分


23 第 28 行与第 38 行分别有可能执行两次及以上。( ) 1.5分
24 当输入为“5 -10 11 -9 5 -7”时,输出的第二行为“7”。( ) 1.5分
25 solve1(1, n) 的时间复杂度为( ) 3分
26 solve2(1, n) 的时间复杂度为( )。 3分
27 当输入为“10 -3 2 10 0 -8 9 -4 -5 9 4”时,输出的第一行为( )。 3分
28
第 28 - 33 题 组合题


假设输入总是合法的(一个整数和一个不含空白字符的字符串,用空格隔开),完成下面的判断题和单选题:
程序总是先输出一行一个整数,再输出一行一个字符串。( )
1.5分


29
对于任意不含空白字符的字符串 str1,先执行程序输入“0 str1”,得到输出的第
二行记为 str2;再执行程序输入“1 str2”,输出的第二行必为 str1。( )
1.5分
30 当输入为“1 SGVsbG93b3JsZA==”时,输出的第二行为“HelloWorld”。( ) 1.5分
31 设输入字符串长度为 n,encode 函数的时间复杂度为( ) 3分
32 输出的第一行为( )。 3分
33 当输入为“0 CSP2021csp”时,输出的第二行为( )。 3分
完善程序 共10道
34
第 34 - 38 题 组合题
(分数背包)小S有n块蛋糕,编号从1到n第i块蛋糕的价值是wi, 体积是vi。他有一个大小为B的盒子来装这些
蛋糕,也就是说装入盒子的 蛋糕的体积总和不能超过B。
他打算选择一些蛋糕装入盒子,他希望盒子里装的蛋糕的价值之和尽量 大。
为了使盒子里的蛋糕价值之和更大,他可以任意切割蛋糕。具体来说,他 可以选择一个a (0<a<l),并将一块
价值是w,体枳为v的蛋糕切割成两 块.其中一块的价值是a・w,体枳是a・v,另一块的价值是(l-a)・w.体 积是
(l-a)v。他可以重复无限次切割操作。
现要求编程输出最大可能的价值,以分数的形式输出。
比如n=3, B=8,三块蛋糕的价值分别是4、4、2,体枳分别是5、3、2。 那么最优的方案就是将休积为5的蛋糕
切成两份,一份体积是3,价值是 2.4,另一份体积是2,价值是1.6,然后把休积是3的那部分和后两块蛋 糕打包进盒
子。最优的价值之和是8.4,故程序输出42/5。
输入的数据范围为:1≤n≤1000,1≤B≤10^5;1≤wi,vi≤100。
提示:将所有的蛋糕按照性价比wi/vi从大到小排序后进行贪心选择。
试补全程序。


①处应填()
3分
第 34 - 38 题 组合题
(分数背包)小S有n块蛋糕,编号从1到n第i块蛋糕的价值是wi, 体积是vi。他有一个大小为B的盒子来装这些
蛋糕,也就是说装入盒子的 蛋糕的体积总和不能超过B。
他打算选择一些蛋糕装入盒子,他希望盒子里装的蛋糕的价值之和尽量 大。
为了使盒子里的蛋糕价值之和更大,他可以任意切割蛋糕。具体来说,他 可以选择一个a (0<a<l),并将一块
价值是w,体枳为v的蛋糕切割成两 块.其中一块的价值是a・w,体枳是a・v,另一块的价值是(l-a)・w.体 积是
(l-a)v。他可以重复无限次切割操作。
现要求编程输出最大可能的价值,以分数的形式输出。
比如n=3, B=8,三块蛋糕的价值分别是4、4、2,体枳分别是5、3、2。 那么最优的方案就是将休积为5的蛋糕
切成两份,一份体积是3,价值是 2.4,另一份体积是2,价值是1.6,然后把休积是3的那部分和后两块蛋 糕打包进盒
子。最优的价值之和是8.4,故程序输出42/5。
输入的数据范围为:1≤n≤1000,1≤B≤10^5;1≤wi,vi≤100。
提示:将所有的蛋糕按照性价比wi/vi从大到小排序后进行贪心选择。
试补全程序。


①处应填()
35 ②处应填() 3分
36 ③处应填() 3分
37 ④处应填() 3分
38 ⑤处应填() 3分
39
第 39 - 43 题 组合题
(最优子序列)取m=6,给出长度为n的整数序列a1,a2,……an(0 ≤ ai<2m)。对于一个二进制数x,定义其分
值w(x)为x + popcnt(x),其中 popcnt(x)表示x二进制表示中1的个数。对于一个子序列b1,b2,…,bk,定 义其
子序列分值S为w(b1㊉b2)+w(b2㊉b3)+w(b3㊉b4)+……+w(bk-1㊉bk)。其中㊉表示按位异或。对于
空子序列,规定其子序列分值为0。求一个子序列使得其子序列分值最大,输出这个最大值。
输入第一行包含一个整数n(1 ≤ n ≤ 40000).接下来一行包含n个整数 a1,a2,……,an。
提示:考虑优化朴素的动态规划算法,将前 位和后 位分开计算。
Max[x][y]表示当前的子序列下一个位置的高8位是X、最后一个位置的 低8位是y时的最大价值。
试补全程序。
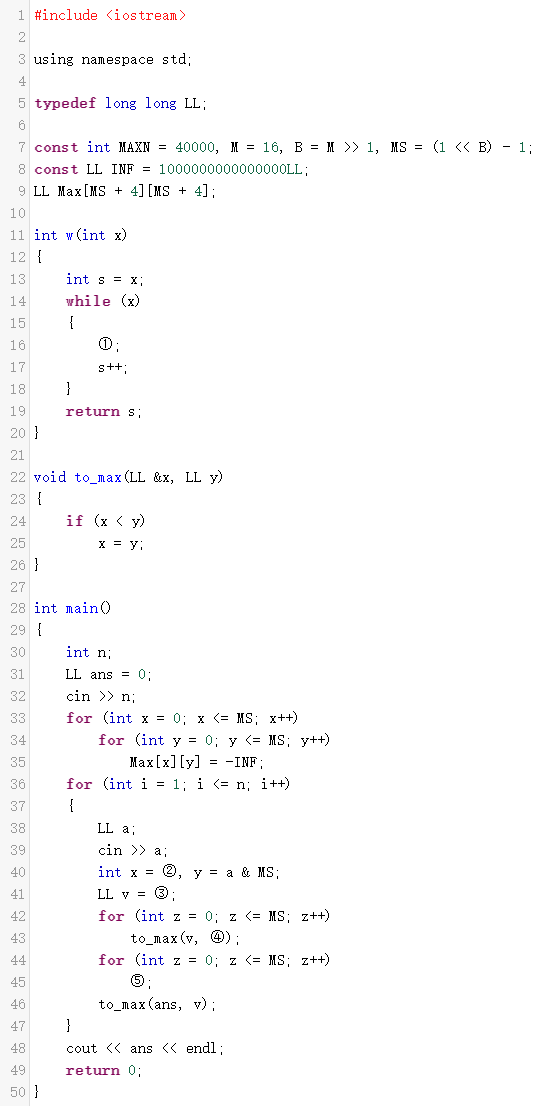
①处应填()
3分
第 39 - 43 题 组合题
(最优子序列)取m=6,给出长度为n的整数序列a1,a2,……an(0 ≤ ai<2m)。对于一个二进制数x,定义其分
值w(x)为x + popcnt(x),其中 popcnt(x)表示x二进制表示中1的个数。对于一个子序列b1,b2,…,bk,定 义其
子序列分值S为w(b1㊉b2)+w(b2㊉b3)+w(b3㊉b4)+……+w(bk-1㊉bk)。其中㊉表示按位异或。对于
空子序列,规定其子序列分值为0。求一个子序列使得其子序列分值最大,输出这个最大值。
输入第一行包含一个整数n(1 ≤ n ≤ 40000).接下来一行包含n个整数 a1,a2,……,an。
提示:考虑优化朴素的动态规划算法,将前 位和后 位分开计算。
Max[x][y]表示当前的子序列下一个位置的高8位是X、最后一个位置的 低8位是y时的最大价值。
试补全程序。

①处应填()