选择题 共15道
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15阅读程序 共17道
16 17 18 19 20 21 22 23 24 25 26 27 29 30 31 32 33完善程序 共10道
34 35 36 37 38 39 40 41 42 43P718 2020年CCF非专业级别软件能力认证第一轮 (CSP-S)提高级C++语言试题-练习
选择题 共15道
01 请选出以下最大的数( ) 2分
02 操作系统的功能是()。 2分
03 现有一段8分钟的视频文件,它的播放速度是每秒24帧图像,每帧图像是 一幅分辨率为2048x1024像素的32位真彩色图像。请问要存储这段原始无 压缩视频.需要多大的存储空间?()。 2分
04 今有一空栈S,对下列待进栈的数据元素序列a,b,c,d,e,f依次进行:进 栈,进栈,出栈,进栈,进栈,出栈的操作,则此操作完成后,栈底元素为( ) 2分
05 将(2, 7, 10, 18)分别存储到某个地址区间为如0~10的哈希表中,如果 哈希函数h(x)=(),将不会产生冲突,其中a mod b表示a除以b的 余数。 2分
06 下列哪些问题不能用贪心法精确求解?( ) 2分
07 具有n个顶点,e条边的图釆用邻接表存储结构,进行深度优先遍历运算的 时间复杂度为() 2分
08 二分图是指能将顶点划分成两个部分,每一部分内的顶点间没有边相连的简单无向图。那么,24个顶点的二分图至多有()条边。 2分
09 广度优先搜索时,一定需要用到的数据结构是() 2分
10 一个班学生分组做游戏,如果每组三人就多两人,每组五人就多三人,每组七人就多四人,问这个班的学生人数n在以下哪个区间?己知n<60。() 2分
11 小明想通过走楼梯来锻炼身体,假没从第1层走到第2层消耗10卡热量,接着从第2层走到第3层消耗20卡热量,再从第3层走到第4层消耗30 卡热量,依此类推,从第k层走到第k+1层消耗10K卡热量(k>l)。如果小 明想从1层开始,通过连续向上爬楼梯消耗1000卡热量,至少要爬到第几 层楼? ( ) 2分
12 表达式a*(b+c)-d的后缀表达形式为( ) 2分
13 从一个4X4的棋盘中选取不在同一行也不在同一列上的两个方格,共有 ()种方法。 2分
14 对一个n个顶点、m条边的带权有向简単图用Dijkstra算法计算単源最短 路时,如果不使用堆或其它优先队列进行优化,则其时间复杂度为()。 2分
15 1948年,()将热力学中的熵引入信息通信领域,标志着信息论研究的 开端。 2分
阅读程序 共17道
16

假设输入的n和d[i]都是不超过10000的正整数,完成下面的判断题和单 选题:
n必须小于1000,否则程序可能会发生运行错误。()
2分

17 输出一定大于等于0。() 2分
18 若将第13行的“j =0”改为“j = i +1” 程序输出可能会改变。() 2分
19 将第14行的“d[i] < d[j]"改为wd[i] != d[j]”,程序输出不会改 变。() 2分
20 若输入n 100.且输出为127.则输入的d[i]中不可能有()。 2分
21 若输出的数大于0,则下面说法正确的是()。 2分
22

假设输入的n, k和d[i]都是不超过10000的正整数,且k不超过n,并 假设rand()函数产生的是均匀的随机数,完成下面的判断题和单选题:
第9行的“x”的数值范围是L+1到R.即[L+l, R]。()
2分

23 将第19行的“d[a]”改为“d[b]“,程序不会发生运行错误。() 2分
24 (2.5分)当输入的d[i]是严格单调递增序列时,第17行的 “swap”平均执行次数是()。 2分
25 (2.5分)当输入的d[i]是严格单调递减序列时,第17行的“swap” 平均执行次数是()。 2分
26 (2.5分)若输入的d[i]为i,此程序①平均的时间复杂度和②最坏 情况下的时间复杂度分别是() 2分
27 (2.5分)若输入的d[i]都为同一个数,此程序平均的时间复杂度是() 2分
29 若输入的两个字符串长度均为101时,则m=0时的输出, m=10O时的 输出是一样的。() 2分
30 若两个字符串的长度均为n,则最坏情况下,此程序的时间复杂度为 0(n!)。 () 2分
31 (2.5分)若输入的第一个字符串长度由100个不同的字符构成,第二 个字符串是第一个字符串的倒序,输入的m为0,则输岀为()。 2分
32 (4分)已知当输入为“0123\n3210\n1”时输出为4,当输入为 “012345\n543210\n1”时输出为14,当输入为 “01234567\n76543210\n1”时输出为28,则当输入为 “0123456789ab\nba9876543210\n1” 输出为()。其中“\n”为换行符。 2分
33 (4分)若两个字符串的长度均为n, 且0<m<n-1,且两个字符串的构 成相同(即任何一个字符在两个字符串中出现的次数均相同),则下列 说法正确的是()。提示:考虑输入与输出有多少对字符前后顺序不 一样。 2分
完善程序 共10道
34
(分数背包)小S有n块蛋糕,编号从1到n第i块蛋糕的价值是wi, 体积是vi。他有一个大小为B的盒子来装这些蛋糕,也就是说装入盒子的 蛋糕的体积总和不能超过B。
他打算选择一些蛋糕装入盒子,他希望盒子里装的蛋糕的价值之和尽量 大。
为了使盒子里的蛋糕价值之和更大,他可以任意切割蛋糕。具体来说,他 可以选择一个a (0<a<l),并将一块价值是w,体枳为v的蛋糕切割成两 块.其中一块的价值是a・w,体枳是a・v,另一块的价值是(l-a)・w.体 积是(l-a)v。他可以重复无限次切割操作。
现要求编程输出最大可能的价值,以分数的形式输出。
比如n=3, B=8,三块蛋糕的价值分别是4、4、2,体枳分别是5、3、2。 那么最优的方案就是将休积为5的蛋糕切成两份,一份体积是3,价值是 2.4,另一份体积是2,价值是1.6,然后把休积是3的那部分和后两块蛋 糕打包进盒子。最优的价值之和是8.4,故程序输出42/5。
输入的数据范围为:1≤n≤1000,1≤B≤10^5;1≤wi,vi≤100。
提示:将所有的蛋糕按照性价比wi/vi从大到小排序后进行贪心选择。
试补全程序。
#include <cstdio>
using namespace std;
const int maxn = 1005;
int n,B, w[maxn], v[maxn];
int gcd(int u, int v) {
if(v == 0)
return u;
return gcd(v, u % v);
}
void print(int w, int v) {
int d = gcd(w> v);
w = w / d;
v = v / d;
if(v == 1)
printf(”%d\n”, w);
else
printf(”%d/%d\n”, w, v);
}
void swap(int &x, int &y) {
int t = x; x = y; y = t;
}
int main() {
scanf("%d %d", &n, &B);
for(int i = 1; i <= n; i ++) {
scanf(”%d%d,&w[i], &v[i]);
}
for(int i = 1; i < n; i ++)
for(int j = 1; j < n; j ++)
if(①){
swap(w[j], w[j + 1]);
swap(v[j],v[j + 1]);
}
int curV, curW;
if(②) {
③
} else {
print(B * w[1], v[1]);
return 0;
}
for(int i = 2; i <= n; i ++)
if(curV + v[i] <= B) {
curV += v[i];
curW += w[i];
} else {
print(④);
return 0;
}
print (⑤);
return 0;
}
①处应填()
2分
35 ②处应填() 2分
36 ③处应填() 2分
37 ④处应填() 2分
38 ⑤处应填() 2分
39
(最优子序列)取m=6,给出长度为n的整数序列a1,a2,……an(0 ≤ ai<2m)。对于一个二进制数x,定义其分值w(x)为x + popcnt(x),其中 popcnt(x)表示x二进制表示中1的个数。对于一个子序列b1,b2,…,bk,定 义其子序列分值S为w(b1㊉b2)+w(b2㊉b3)+w(b3㊉b4)+……+w(bk-1㊉bk)。其中㊉表示按位异或。对于空子序列,规定其子序列分值为0。求一个子序列使得其子序列分值最大,输出这个最大值。
输入第一行包含一个整数n(1 ≤ n ≤ 40000).接下来一行包含n个整数 a1,a2,……,an。
提示:考虑优化朴素的动态规划算法,将前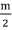 位和后
位和后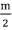 位分开计算。
位分开计算。
Max[x][y]表示当前的子序列下一个位置的高8位是X、最后一个位置的 低8位是y时的最大价值。
试补全程序。

①处应填()
2分
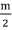 位和后
位和后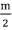 位分开计算。
位分开计算。